- Главная
- Сведения об образовательной организации
- Основные сведения
- Структура и органы управления образовательной организацией
- Документы
- Образование
- Образовательные стандарты
- Руководство Педагогический состав
- Материально-техническое обеспечение и оснащенность образовательного процесса
- Стипендия и иные виды материальной поддержки
- Платные образовательных услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приема (перевода)
- Публичный отчет
- Предписания органов, осуществляющих государственный контроль в сфере образования
- Отчет о результатах самообследования
- Документы
- Образовательный процесс
- Родителям
- Федеральный образовательный портал
- Росийский общеобразовательный портал
- Официальный портал ЕГЭ 2015
- Портал дополнительного образования
- РИАЦ
- Родителям будущих первоклассников
- ЕГЭ и ГИА
- Платные образовательные услуги
- Модернизация школы
- График проведения встреч классных руководителей
- Наши планы и проекты
- Финансовы отчет ФСО "Школьник"
- Карта сайта






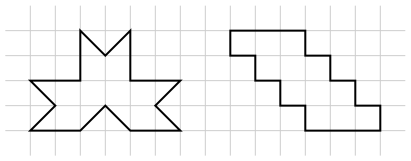
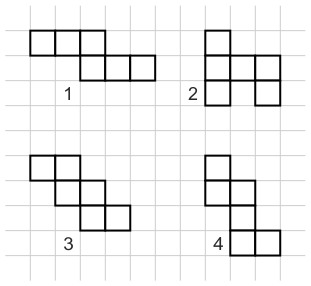

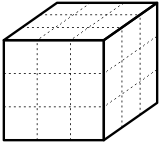
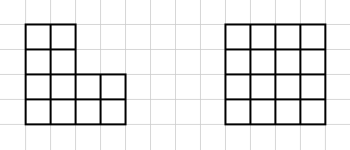
Комментариев нет:
Отправить комментарий